CARACTERIZACIÓN DE VARIABLES CUANTITATIVAS

Los datos cuantitativos se pueden trabajar como datos sueltos cuando no son demasiados o cuando no son tan distintos unos de otros. De lo contrario lo mas recomendado es agruparlos en tablas de frecuencia con o sin intervalos.

CARACTERIZACIÓN DE DATOS NO AGRUPADOS 

Cuando tiene un listado de datos es importante reconocer simultáneamente el valor individual a los datos mas representativos de cada una de las observaciones. Para tal fin se usa el diagrama de tallos y hojas y las medidas numéricas descriptivas.

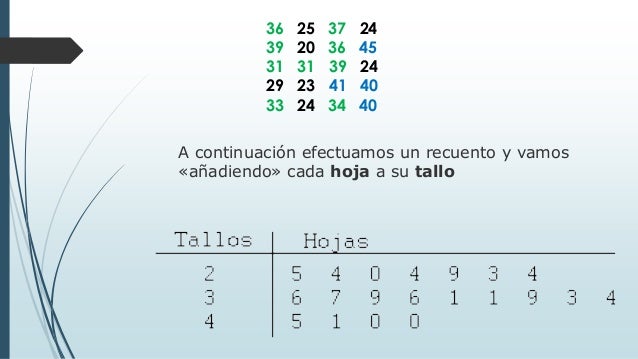
DIAGRAMA  DE TALLO Y HOJAS

Es una tecnica que se usa para organizar y recontar los datos.

-este diagrama consta de dos columnas: tallo y hojas. 

MEDIDAS NUMÉRICAS DESCRIPTIVAS PARA DATOS NO AGRUPADOS

Existen  varias medidas  de interes que permiten describir un grupo de observaciones dentro de las cuales estan las medidas de tendencia central, medidas de posición y medidas de .dispercion.

MEDIDAS DE MEDIDA CENTRAL

Son medidas dentro de un conjunto de observaciones que establecen la posición de los datos para agruparse ya sea alrededor del centro de ciertos  valores numéricos. Las medidas de tendencia central son...La Media, La Mediana y La Moda.

MEDIA ARITMÉTICA O PROMEDIO

MEDIA: también llamada promedio o media, de un conjunto finito de números es el valor característico de una serie de datos cuantitativos, objeto de estudio que parte del principio de la esperanza matemática o valor esperado, se obtiene a partir de  la suma de todos sus valores dividida entre el número de sumandos. Cuando el conjunto es una muestra aleatoria recibe el nombre de media muestral siendo uno de los principales estadísticos muestrales.

Dados los n números , la media aritmética se define como:

${\displaystyle {\bar {x}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}={\frac {x_{1}+x_{2}+\cdots +x_{n}}{n}}}$

Por ejemplo, la media aritmética de 8, 5 y -1 es igual a:

${\displaystyle {\bar {x}}={\frac {8+5+\left(-1\right)}{3}}=4}$

Se utiliza la letra x con una barra horizontal sobre el símbolo para representar la media de una muestra

 (), mientras que la letra µ (mu) se usa para la media aritmética de una población, es decir, el valor esperado de una variable.

En otras palabras, es la suma de n valores de la variable y luego dividido por n, donde n es el número de sumandos, o en el caso de estadística el número de datos se da el resultado.

MEDIANA: En el ámbito de la estadística, la mediana  representa el valor de la variable de posición central en un conjunto de datos ordenados.

Cálculo de la mediana:

1- Ordenamos los datos de menor a mayor.

2- Si la serie tiene un número impar de medidas la mediana es la puntuación central.

2, 3, 4, 4, 5, 5, 5, 6, 6 Mediana = 5

3. Si la serie tiene un número par de puntuaciones la mediana es la media entre las dos puntuaciones centrales.

7, 8, 9, 10, 11, 12 Me = 9,5

Existen dos métodos para el cálculo de la mediana:

1. Considerando los datos en forma individual, sin agruparlos.
2. Utilizando los datos agrupados en intervalos de clase.

A continuación veamos cada una de ellas:

Datos sin agrupar

Sean ${\displaystyle x_{1},x_{2},x_{3},\ldots ,x_{n}}$ los datos de una muestra ordenada en orden creciente y designando la mediana como ${\displaystyle M_{e}}$, distinguimos dos casos:

a) Si n es impar, la mediana es el valor que ocupa la posición ${\displaystyle (n+1)/2}$ una vez que los datos han sido ordenados (en orden creciente o decreciente), porque éste es el valor central. Es decir: ${\displaystyle M_{e}=x_{(n+1)/2}}$.

Por ejemplo, si tenemos 5 datos, que ordenados son: ${\displaystyle x_{1}=3}$, ${\displaystyle x_{2}=6}$, ${\displaystyle x_{3}=7}$, ${\displaystyle x_{4}=8}$, ${\displaystyle x_{5}=9}$ => El valor central es el tercero: ${\displaystyle x_{(5+1)/2}=x_{3}=7}$. Este valor, que es la mediana de ese conjunto de datos, deja dos datos por debajo (${\displaystyle x_{1}}$, ${\displaystyle x_{2}}$) y otros dos por encima de él (${\displaystyle x_{4}}$, ${\displaystyle x_{5}}$).

b) Si n es par, la mediana es la media aritmética de los dos valores centrales. Cuando ${\displaystyle n}$ es par, los dos datos que están en el centro de la muestra ocupan las posiciones ${\displaystyle n/2}$ y ${\displaystyle (n/2)+1}$. Es decir: ${\displaystyle M_{e}=(x_{\frac {n}{2}}+x_{{\frac {n}{2}}+1})/2}$.

Por ejemplo, si tenemos 6 datos, que ordenados son: ${\displaystyle x_{1}=3}$, ${\displaystyle x_{2}=6}$, ${\displaystyle x_{3}=7}$, ${\displaystyle x_{4}=8}$, ${\displaystyle x_{5}=9}$, ${\displaystyle x_{6}=10}$. Aquí dos valores que están por debajo del ${\displaystyle x_{\frac {6}{2}}=x_{3}=7}$ y otros dos que quedan por encima del siguiente dato ${\displaystyle x_{{\frac {6}{2}}+1}=x_{4}=8}$. Por tanto, la mediana de este grupo de datos es la media aritmética de estos dos datos: ${\displaystyle M_{e}={\frac {x_{3}+x_{4}}{2}}={\frac {7+8}{2}}=7,5}$.

Datos agrupados

Al tratar con datos agrupados, si ${\displaystyle {\frac {n}{2}}}$ coincide con el valor de una frecuencia acumulada, el valor de la mediana coincidirá con la abscisa correspondiente. Si no coincide con el valor de ninguna abscisa, se calcula a través de semejanza de triángulos en el histograma o polígono de frecuencias acumuladas, utilizando la siguiente equivalencia:

${\displaystyle {\frac {N_{i}-N_{i-1}}{a_{i}-a_{i-1}}}={\frac {{\frac {n}{2}}-N_{i-1}}{p}}\Rightarrow p={\frac {{\frac {n}{2}}-N_{i-1}}{N_{i}-N_{i-1}}}(a_{i}-a_{i-1})}$

Donde ${\displaystyle N_{i}}$ y ${\displaystyle N_{i-1}}$ son las frecuencias absolutas acumuladas tales que ${\displaystyle N_{i-1}<{\frac {n}{2}}<N_{i}}$, ${\displaystyle a_{i-1}}$ y ${\displaystyle a_{i}}$ son los extremos, interior y exterior, del intervalo donde se alcanza la mediana y ${\displaystyle M_{e}=a_{i-1}+p}$ es la abscisa a calcular, la mediana. Se observa que ${\displaystyle a_{i}-a_{i-1}}$ es la amplitud de los intervalos seleccionados para el diagrama.

Ejemplos para datos sin agrupar

Ejemplo 1: cantidad (N) impar de datos[

xi	fi	Ni
1	2	2
2	2	4
3	4	8
4	5	13
5	8	21 > 19,5
6	9	30
7	3	33
8	4	37
9	2	39

Las calificaciones en la asignatura de Matemáticas de 39 alumnos de una clase viene dada por la siguiente tabla:

Calificaciones	1	2	3	4	5	6	7	8	9
Número de alumnos	2	2	4	5	8	9	3	4	2

Primero se hallan las frecuencias absolutas acumuladas ${\displaystyle N_{i}}$. Así, aplicando la fórmula asociada a la mediana para n impar, se obtiene ${\displaystyle X(39+1)/2=X20}$.

• Ni-1< n/2 < Ni = N19 < 19,5 < N20

Por tanto la mediana será el valor de la variable que ocupe el vigésimo lugar.En este ejemplo, 21 (frecuencia absoluta acumulada para Xi = 5) > 19,5 con lo que Me = 5 puntos, la mitad de la clase ha obtenido un 5 o menos, y la otra mitad un 5 o más.

Ejemplo 2: cantidad (N) par de datos

Las calificaciones en la asignatura de Matemáticas de 38 alumnos de una clase viene dada por la siguiente tabla (debajo):

Calificaciones	1	2	3	4	5	6	7	8	9
Número de alumnos	2	2	4	5	6	9	4	4	2

xi	fi	Ni+w
1	2	2
2	2	4
3	4	8
4	5	13
5	6	19 = 19
6	9	28
7	4	32
8	4	36
9	2	38

Primero se hallan las frecuencias absolutas acumuladas ${\displaystyle N_{i}}$. Así, aplicando la fórmula asociada a la mediana para n par, se obtiene la siguiente fórmula: ${\displaystyle X=n/2==>X=(38/2)=>X=19}$ (Donde n= 38 alumnos divididos entre dos).

• Ni-1< n/2 < Ni = N18,5 < 19 < N19,5

Con lo cual la mediana será la media aritmética de los valores de la variable que ocupen el decimonoveno y el vigésimo lugar. En el ejemplo el lugar decimonoveno lo ocupa el 5 y el vigésimo el 6 con lo que Me = (5+6)/2 = 5,5 puntos, la mitad de la clase ha obtenido un 5,5 o menos y la otra mitad un 5,5 o más.

MEDIDAS DE POSICIÓN

Son  números que dividen el conjunto de datos en partes iguales y se usa para clasificar una observación dentro de una población o muestra, dentro de esta medida se encuentra los Cuartiles, Desiles y Persentines.

u PERCENTILES: son 99 valores que dividen en cien partes iguales el conjunto de datos ordenados. Ejemplo, el percentil de orden 15 deja por debajo al 15% de las observaciones, y por encima queda el 85%

•

 u CUARTILES: son los tres valores que dividen al conjunto de datos ordenados en cuatro partes iguales, son un caso particular de los percentiles:

- El primer cuartil Q 1 es el menor valor que es mayor que una cuarta parte de los datos - El segundo cuartil Q 2 (la mediana), es el menor valor que es mayor que la mitad de los datos - El tercer cuartil Q 3 es el menor valor que es mayor que tres cuartas partes de los datos

 u DECILES: son los nueve valores que dividen al conjunto de datos ordenados en diez partes iguales, son también un caso particular de los percentiles.

OTRAS MEDIDAS NUMÉRICAS DESCRIPTIVAS PARA DATOS NO AGRUPADOS

Las medidas de tendencia central tienen como objetivo el sintetizar los datos en un valor representativo, las medidas de dispersión nos dicen hasta que punto estas medidas de tendencia central son representativas como síntesis de la información. Las medidas de dispersión cuantifican la separación, la dispersión, la variabilidad de los valores de la distribución respecto al valor central. Distinguimos entre medidas de dispersión absolutas, que no son comparables entre diferentes muestras y las relativas que nos permitirán comparar varias muestras.

RANGO: Es la diferencia entre  el dato mayor y el menor del conjunto de datos. Permite visualizar la amplitud de la distribución de los datos.

VARIANZA: ( s² ): es el promedio del cuadrado de las distancias entre cada observación y la media aritmética del conjunto de observaciones.


DESVIACION ESTANDAR:(S): La varianza viene dada por las mismas unidades que la variable pero al cuadrado, para evitar este problema podemos usar como medida de dispersión la desviación típica que se define como la raíz cuadrada positiva de la varianza.