PROBABILIDAD
QUE ES LA PROBABILIDAD?
La probabilidad estudia experimentos en los que se pueden esperar varios resultados y no solamente uno. los experimentos se pueden clasificar en:
Aleatorio y Deterministico.
EXPERIMENTO DETERMINISTICO:
Es un ensayo en el que se sabe previamente el resultado.
EXPERIMENTO ALEATORIO:
Es una accion cuyo resultado sea aleatorio debe reunir las 3 condiciones:
- Antes de realizar el experimento se deben conocer todos los posibles resultados
- No es posible predecir un resultado en particular
- El experimento se puede ejecutar infinitas veces con las mismas condiciones
ESPACIO MUESTRAL S :
Es el conjunto que une todos los posibles resultados que puede tener un experimento Aleatorio.
A cada uno de los resultados del espacio muestral se le denomina Punto Muestral.
EVENTO
Un evento es cualquier subconjunto del espacio muestral cuyos elementos tienen una característica en común. Se simbolizan con letras mayúsculas
- Los eventos son conjuntos se los puede aplicar operaciones y propiedades de la teoría de conjuntos.
EVENTO SIMPLE O ELEMENTAL:
Es aquel subconjunto un solo punto muestral.
EVENTO COMPUESTO:
Es un subconjunto con mas de un punto muestral.
EVENTO IMPOSIBLE:
Es un subconjunto de S que no contiene ningún punto muestral, es decir un subconjunto vació.
EVENTO SEGURO:
Subconjunto que contiene los mismos puntos del espacio muestral S.
UNION DE EVENTOS:
Se ocurre por lo menos uno o varios eventos a la vez. Asi, se ocurre el evento E o el evento F, entonces, ocurre el elemento EuF.
INTERSECCIÓN DE EVENTOS:
Si los eventos ocurren al mismo tiempo, es decir, si ocurre el evento G y el evento H, GnH.
EVENTO MUESTRAL EXCLUYENTES:
Son subconjunto cuya interseccion es vacia.

CALCULO DE PROBABILIDADES
Para calcular probabilidades se utiliza la siguiente fórmula:
Probabilidad = Casos favorables / Casos posibles
El resultado se multiplica por 100 para expresarlo en porcentaje.
Veamos algunos ejemplos:
a) Calcular la probabilidad de que salga "cara" al lanzar una moneda:
- Casos favorables: 1 (que salga "cara")
- Casos posibles: 2 (puede salir "cara" o "cruz")
- Probabilidad = (1 / 2 ) x 100 = 50 %
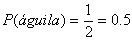
- Por lo tanto, existe una probabilidad del 50% que yo obtenga un águila al tirar una moneda.
- Veamos otro ejemplo: Si yo tengo una canasta llena de peras y manzanas, de las cuales hay 20 peras y 10 manzanas. ¿Qué fruta es más probable que saque al azar de la canasta?
- Para este ejemplo tenemos que 30 es el total de frutas en la canasta; es decir los casos posibles. Para calcular la probabilidad de sacar una manzana mis casos favorables son 10 puesto que existen sólo 10 manzanas. Así, aplicando la fórmula obtenemos que:
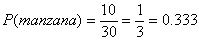 ó 33.3% probable
ó 33.3% probable - Calculando igual, la probabilidad de sacar pera es:
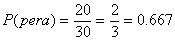 ó 66.7% probable
ó 66.7% probable - Como 66.7 es mayor que 33.3 es más probable que saque una pera, pues hay más peras que manzanas en la canasta.
- Fíjate bien que 33.3% + 66.7% es igual al 100% porque siempre que saques algo de la canasta es seguro que saques una fruta.
- Así, el valor de la probabilidad de un evento imposible es 0 mientras que la probabilidad de un evento seguro es 1; porque:
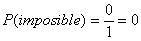
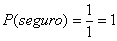
Comentarios
Publicar un comentario